Query Processing

A quick primer on the relational algebra

• selection
• projection
• cartesian product
• union
• difference
• join (in particular, theta-join)

Dataflow Architecture: Iterators

An OO view of iterators:

• open(): initialize state to set up dataflow.
• next(): produce a record as output
• close(): clean up state

Iterators are strung together into a dataflow by parameterizing them to have other iterators as inputs, and then having their methods invoke the input iterators' methods.  Usually parent.open() invokes child.open() and sometimes child.next().  Usually parent.next() invokes child.next() or nothing.  Usually parent.close() invokes child.close().

An iterator also has a number of private data members, including all the "input" iterators it invokes (usually one or two of these), and any state it maintains.  The types of the records from input iterators need to match the operator semantics in generating the output type.  In a DBMS, this is all set up automatically at query parsing/optimization time.  Extensible "optimizer generators" have been developed that let you declare these rules in a high-level way (not as optimizer code).

A state-machine/event-handler view:

An eventflow graph is constructed to string together the dataflow, and type matching of tuples needs to be managed as part of constructing that graph.
 

A note on Synchronous/Asynchronous (a.k.a. Pull/Push)

As we'll see later this semester, in some contexts it can be more efficient to "push" the data between iterators (e.g. if there's a network in between!).  This means that tuples arrive asynchronously.  Some kind of buffering and/or rate-matching has to happen to keep operators in sync.

Typical DB Dataflow Operators

Unary Operations

• sorting: see Knuth, or Shapiro paper. Then follow up at Jim Gray's Sort Benchmark homepageUses?
• hashing: a minor variant of hybrid-hash join works well. Uses?

Binary Operations: Union

With duplicate elimination (SQL's plain "UNION"), you need to eliminate duplicates too.  Simple implementation: do UNION ALL as one iterator, and dup-elim as another; make sure to use them in order if somebody wants UNION without dups.

Binary Operations: Join

Some commonly used join variants (alternative logical algebra operators):

• semi-join: R semi-join S ~= R join remove-dups(S) projected to the columns of R
• S basically serves as a filter
• logically, selection is a semijoin with an infinite relation (!!)
• outer join: R outer-join S: compute R join S, and for each tuple of R that has no match send it to the output with the S columns filled in with NULLs. Left, Right, and Full Outer Joins exist.  Very common for web apps.  Some logical subtleties here (no longer commutative/associative).
• intersection & difference

The "Guy Lohman Test" for join operators (a.k.a. pipelining of intermediate results):

• does the operator work for joining 3 inputs without storing the output of 2 of the inputs?

• does the operator produce outputs before it finishes reading any of its inputs?
• how quickly -- and are they the juicy outputs?

Nested Loops Join

for each tuple r of R
    for each tuple s of S
       if rs satisfies join predicate
          output rs

S is the inner relation (right)

• works for any join predicate
• inner input must be stored

Refinement 1: Block Nested Loops Join

for each block BR of R
    for each tuple s of S
        for each tuple r of BR such that rs satisfies join predicate
               output rs

• load R in chunks of M-K pages to amortize seek cost, "pin" K pages of the inner into memory
• alternate scan direction on inner ("boustrophedonism")

Refinement 2: Index Nested Loops Join

for each tuple r of R
    probe index over S;
    output all s s.t. rs satisfies join predicate;

• Still called "nested loops", S is still referred to as the "inner" relation
• any join predicate can be supported if the index supports the predicate!

        SELECT cities.name
          FROM cities, forests
         WHERE cities.boundary overlaps forests.boundary;

• can convert all nested-loops joins to index-nested-loops by indexing inner on the fly.  usually not worth it.

(Sort-)Merge Join

we will assume here you know how to do a 2-pass sort [see Knuth or Shapiro]

idea: if R & S are sorted on the join column(s), we can "simply" merge them

But duplicates complicate things (as usual).
 

R	S	R join S
1	1	1,1
2	2	2,2
2	4	2,2
3	5	5,5
5	5	5,5

sort R;
sort S;
R.open();
S.open();
r = R.next();
s = S.next();
while (r != NULL && s != NULL) {
    while (r.c < s.c)
        r = R.next();
    if (r.c = s.c) {
        while (r.c = s.c) {
            output rs;
            r = R.next();
        }
        "rewind" r to first tuple of R where r.c = s.c;
        s = S.next();
    }
    while (r.c > s.c)
        s = S.next();
}

• Requires enough buffers for merging both R and S simultaneously.

Classic Hash Join

Let R be the smaller relation

Hash R into VM;
for each tuple of S
    probe hashtable over R and output all rs s.t. s.c = r.c

• In the spirit of indexed nested-loop join, S is "outer" (left), and R is "inner" (right)
• Warning: at least one important paper calls S the right relation, R the left!!!
• I prefer to call S left/outer, R right/inner
 
• note that hash join is very similar to nested-loop + index-on-the-fly (which Sybase used to do.)  If we call the probing relation there the "outer", we should do the same here!
• Safest to refer to "building" and "probing" relations

Simple Hash Join

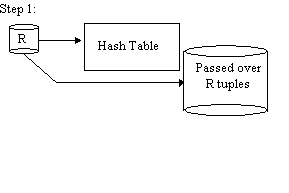
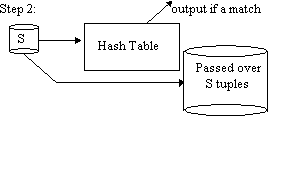
Repeat steps 1 and 2 with R, S replaced by the passed over tuples.

Advantages:

• Great when R is small
• Works for memory of any size

• you tell me!

Grace Hash Join

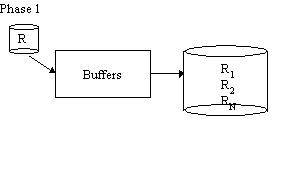
Phase 1 is repeated with S in place of R

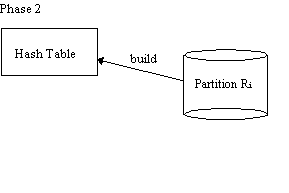   THEN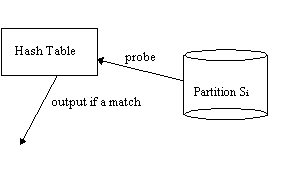 

Advantages:

• works well for big R, esp. when RAM is just big enough for output buffers of R

• you tell me!

Hybrid Hash

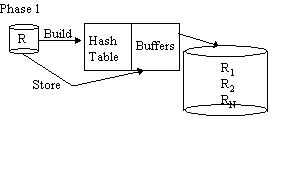
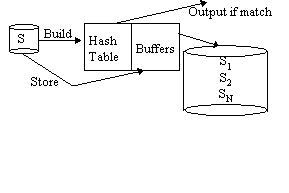
Phase 2 as in Grace Join

Hybrid Hash Advantages:

• As good as simple hash for small R
• As good as Grace for big R
• If RAM is bigger than # of output buffers, improves on Grace

• you tell me

• If a partition of R overflows, recursively partition it, along with the corresponding bucket of S
• Note that size of S does not affect level of recursion!
• Makes hash-join particularly effective if |R| << |S| (compare to sort-merge)

Idea: build a filter based on R so you stage less of S to disk

• Babb Array filter
• Bloom filter


These are like lossy semijoins! Any superset of S semijoin R will do.